Wiskunde is overal om ons heen, waar we ook gaan en staan. Of nou gaat om het bouwen van je huis, het stratenplan in je buurt, een simpele actie als het starten van je auto of de wasmachine, of piano spelen, wiskunde is overal. Misschien kan wiskunde je zelfs helpen om in het casino te winnen bij spellen als Poker en Blackjack!
Welke wiskundige formules zijn er? In dit artikel bespreken we onderstaande formules:
- De stelling van Pythagoras
- Logaritmen
- De wet van de zwaartekracht
- De relativiteitstheorie
- Chaos theorie
- Identiteit van Euler
- De Fourier Transformatie
- Maxwell's vergelijkingen
- De tweede wet van de thermodynamica
- De Schrödinger-vergelijking
Complexe vergelijkingen met veel onbekende wiskundige stellingen, vanaf de oudheid tot ontdekkingen aan het eind van de twintigste eeuw, hebben onze wereld gevormd. Maar hoe werkt een wiskunde vergelijking precies? In een vergelijking worden twee uitdrukkingen aan elkaar gelijkgesteld. De oplossing van een vergelijking houdt in dat we de waarde van de onbekende variabele berekenen.
In 2013 publiceerde de beroemde Britse wiskundige en wetenschapper Ian Stewart een boek genaamd '17 equations that changed the world'. In het Nederlands is dit boek vertaald onder de titel 'Hoe wiskunde de wereld veranderde'. En met elk nieuw concept begrijpen we steeds beter hoe de wereld om ons heen is ontstaan en blijft groeien.

10 van de meest beroemde wiskundige formules en stellingen!
Als je jezelf afvraagt waarom wiskunde zo belangrijk is, en wat de impact van bepaalde wiskundige vergelijkingen is geweest, lees dan verder en ontdek hoe 10 revolutionaire formules wiskunde naar een nieuw niveau hebben gebracht.
Laten we eveneens ook verder kijken wat een wiskunde formule precies inhoudt. Een formule is een wiskundige uitdrukking met variabelen. Het dient om de relatie tussen variabelen te beschrijven of om een rekenkundige regel beknopt weer te geven. Formules worden vaak zo eenvoudig mogelijk weergegeven, waarbij woorden in de formule, de variabelen, meestal worden afgekort tot één letter, bij voorkeur in kleine letters. En als je na dit artikel zelf bent geïnspireerd, kan Superprof je helpen om de perfecte wiskunde leraar te vinden!
1. De stelling van Pythagoras
Dit is absoluut een van de bekendste theorieën. Zelfs jaren na je laatste wiskundeles, blijf je deze naam onthouden. Misschien weet je nog hoe hij werkt, maar anders is hier een geheugensteuntje: in een rechthoekige driehoek is de som van de gekwadrateerde lengtes van de rechthoekszijden gelijk aan de gekwadrateerde lengte van de schuine zijde.
Deze theorie, die afstamt uit 530 voor Christus, is een van de fundamenten van de hedendaagse wiskunde en heeft bijgedragen aan de geschiedenis van de wiskunde sinds de ontdekking. De vergelijking is essentieel om te begrijpen hoe geometrie (meetkunde) en trigonometrie werken, en heeft ons geholpen deze soorten wiskunde beter te begrijpen.
Euclides, een andere Oud-Griekse wiskundige, heeft veel betekend voor de meetkunde.
Dankzij Pythagoras en zijn beroemde vergelijking kunnen we sindsdien lengtes en hoeken makkelijker berekenen, en kunnen we aantonen dat een driehoek daadwerkelijk rechthoekig is. Met name binnen de bouw en architectuur komt dat zeer goed van pas.

Begrijp allerlei wiskunde formules beter door aan wiskunde lessen deel te nemen in de stad naar keuze met je eigen gekozen privéleraar.
2. Logaritmen
Logaritmen, populair geworden dankzij John Napier in 1610, combineren inverse en exponentiële functies en tegenstellingen. Een logaritme wordt vooral gevonden bij formules binnen de scheikunde om de complexiteit van algoritmen en fractals te meten, en ze komen voor in formules om priemgetallen uit te rekenen.
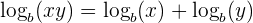
Het logaritme van een product is de som van de logaritmen van de factoren.
Tot de ontwikkeling van de moderne computer was het doen van berekeningen dankzij logaritmen de meest gebruikelijke manier om grote getallen bij elkaar op te tellen, waardoor er sneller berekeningen gemaakt konden worden. Maar boven alles hielpen logaritmen met het maken van nieuwe stappen binnen wiskunde, natuurkunde, astronomie en bouwkunde.
Er bestaan 3 soorten logaritmen:
Natuurlijke logaritmen vormen een fundamentele basis bij het maken van wiskundige analyses
Decimale logaritmen worden gebruikt bij wiskundige berekeningen
Binaire logaritmen worden gebruikt bij computerwetenschappen en toegepaste wiskunde.
Het logaritme van een getal is de exponent waarmee een ander vast getal, de basis, moet worden machtsverheven om het eerste getal te produceren.
Als de basis bijvoorbeeld 10 is, is het logaritme (Log): Log (1) = 0, log (10) = 1, log (100) = 2.
10 tot de macht 2 (10^2) is 100, dus in dit voorbeeld: het logaritme (2) van een getal (100) is de exponent (2) waarmee een ander vast getal, de basis, (10) moet worden machtsverheven om het eerste getal (100) te produceren.
3. De wet van de zwaartekracht
Wie heeft nog nooit gehoord van de beroemde wet van de zwaartekracht van Isaac Newton? Je kent misschien wel het verhaal van de appel die op het hoofd van de grote denker viel toen hij een dutje deed bij maanlicht onder een boom in het jaar 1687.
Door een verband te trekken tussen die twee bollen (de appel en de maan) vroeg Newton zich af: waarom valt de maan niet uit de hemel?
Het antwoord is duidelijk – voor ons inmiddels: de maan 'blijft hangen' door de zwaartekracht.
En zo werd de beroemde wet van de zwaartekracht geboren: "Astrale lichamen trekken elkaar aan met een kracht die evenredig is met hun massa en omgekeerd evenredig met het kwadraat van de afstand tussen hun centra".
200 jaar na Newton heeft Einstein deze wet overigens vervangen met zijn relativiteitstheorie.
4. De relativiteitstheorie
Of je nou je achtergrond hebt in de fysica of wiskunde, of juist onbekend bent met bèta vakken, iedereen kent Albert Einstein's beroemde formule: E = mc². Deze formule, die de relativiteitstheorie (speciale relativiteit en algemene relativiteit) illustreert, gold als een revolutie op het gebied van de natuurkunde op dat moment. Tot op de dag van vandaag is hij cruciaal gebleven, aangezien de theorie aantoont dat materie kan worden omgezet in energie, en vice versa.

Speciale relativiteit introduceert het idee dat de snelheid van het licht een universele constante was die niet veranderde, en dat het verstrijken van de tijd niet hetzelfde was voor verschillende planeten die zich met verschillende snelheden bewogen. Einstein's algemene relativiteit beschrijft de zwaartekracht waarin ruimte en tijd zijn gebonden: een grote verandering in onze kennis na de ontdekkingen gedaan door Newton.
Zelfs vandaag de dag blijft Einstein's relativiteitstheorie nog essentieel in onze kijk op het ontstaan, de structuur en de toekomst van ons universum.
Wiskunde helpt ons de wereld om ons heen beter te begrijpen, en is een aanwezige kracht in ons dagelijks leven.
Wil je beter begrijpen hoe wiskunde en natuurkunde samenkomen in theorieën zoals die van Einstein? Met bijles wiskunde Gent via Superprof ontdek je stap voor stap hoe formules zoals E = mc² werken.
5. Chaos theorie
De chaostheorie heeft aangetoond dat het onmogelijk is om met zekerheid te voorspellen wat er in de toekomst zal gebeuren. Het is een studie van het gedrag van dynamische systemen. Een geweldig onderwerp binnen de wiskunde.

De theorie toont aan dat bestaande processen nooit met zekerheid voorspeld kunnen worden. Hoewel Edward Lorenz als de vader van de chaostheorie wordt gezien, kwam Robert May in 1975 met een variatie op de theorie. Hij beschrijft een proces dat constant evolueert door de jaren heen. In zijn formule wiskunde wilde May uitleggen dat chaotisch gedrag (zoals het klimaat, waarbij er tal van veranderingen in het weer voorkomen, van moment tot moment) kan leiden tot veranderingen in compleet andere systemen, een paar dagen later.
De beste illustratie hiervan is het zogeheten butterfly-effect, dat aantoont dat het wapperen van de vleugels van een vlinder in Brazilië kan leiden tot een orkaan of tornado in Azië.
In andere woorden, de kleinste gebeurtenis kan onverwachte gevolgen hebben op onze omgeving, dichtbij en ver weg.
Het is de optelsom van factoren gerelateerd aan een bepaalde gebeurtenis die zorgt voor onvoorspelbaarheid.
6. Identiteit van Euler
De identiteit van Euler wordt gezien als een van de mooiste vergelijkingen binnen de wiskunde omdat het een ongebruikelijke combinatie van vijf wiskundige constanten beschrijft. De identiteit van Euler (gepubliceerd door Leonhard Euler in 1755) is van toepassing op vloeistof.
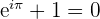
De formule van Euler is de vergelijking waarbij 'e' Euler's nummer is, de basis van natuurlijke logaritmen, 'i' de denkbeeldige eenheid, en '?' is pi, de verhouding van de omtrek van een cirkel tot de diameter. Waarom is deze vergelijking van belang? Omdat het gebruik maakt van drie fundamentele bewerkingen in de rekenkunde: optellen, vermenigvuldigen en machtsverheffingen.
Euler’s formule is de meest opmerkelijke formule in de wiskunde.
Richard Feynman
De vijf constanten zijn: "0", de additieve identiteit; "1", de vermenigvuldigende identiteit; de fantastische pi; "e" wat de basis is van natuurlijke logaritmen en een getal dat veel voorkomt in wiskundige analyses; en "i", de imaginaire eenheid van complexe getallen gevonden in vergelijkingen met 3 onbekende eenheden. Deze vergelijking, die het Palais de la Découverte in Parijs siert, maakte de weg vrij voor de ontwikkeling van topologie, een tak van moderne wiskunde.
7. De Fourier Transformatie
De Fourier transformatie scheidt tijd in verschillende frequenties en golven, zoals een prisma licht in verschillende kleuren splitst.
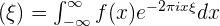
De Fourier transformatie helpt ons niet-periodieke functies te begrijpen.
Een ander voorbeeld is een magnetisch of akoestisch veld, dat we ook wel een signaal noemen. De Fourier transformatie is het spectrum dat zo'n veld ontleedt. De theorie was zo baanbrekend omdat het ineens mogelijk was om meer complexe structuren als de menselijke spraak te begrijpen in de vorm van golven. Vandaag de dag is deze theorie, die werd gepresenteerd in 1822, het fundament van het verwerken en analyseren van alle moderne signalen.
8. Maxwell's vergelijkingen
Maxwell's vergelijkingen beschrijven hoe elektrische ladingen met elkaar in verbinding staan. Daarnaast beschrijven ze elektrische stromen en magnetische velden. Maxwell's vergelijkingen, ook wel Maxwell-Lorentz vergelijkingen genoemd, zijn fundamentele wetten binnen de fysica. Ze liggen aan de basis van onze kennis over de relatie tussen elektriciteit en magnetisme, en vallen onder de meest essentiële, fundamentele wetten binnen de moderne fysica. Er zijn vier verschillende wetten die onder Maxwell's vergelijkingen vallen:

- De Maxwell-Gauss vergelijking (over de samenhang tussen elektrische lading en elektrische flux)
- De Maxwell-flux vergelijking (of Maxwell-Thomson) vergelijking (de elektrische flux door een gesloten oppervlak is altijd nul)
- De Maxwell-Faraday vergelijking (over hoe door een veranderend magnetisch veld een elektrisch krachtveld ontstaat)
- De Maxwell-Ampere vergelijking (over hoe een magnetisch veld wordt opgewekt door elektrische stroom en verplaatsing)
Dankzij deze formules begrijpen we niet alleen elektriciteit en magnetisme beter, maar ook hoe licht eigenlijk een elektromagnetische golf is! Zonder Maxwell hadden we vandaag misschien geen radio, wifi of zelfs je magnetron in de keuken.
9. De tweede wet van de thermodynamica
De tweede wet van de thermodynamica (ook wel bekend als het principe van Carnot, naar zijn ontdekker in 1824) toont dat fysische fenomenen onomkeerbaar zijn, zeker wanneer er zich thermale veranderingen voordoen. Dit principe is meerdere keren aangepast en geherformuleerd, en werd wereldwijd bekend in 1873 dankzij Ludwig Boltzmann en Max Planck.
Daar waar de eerste wet van de thermodynamica aantoont dat energie kan worden uitgewisseld tussen hitte en materie, introduceert de tweede wet een andere hoeveelheid, bekend als entropie. Entropie is gebaseerd op verandering en evolutie, aangezien het laat zien in wat voor richting transformaties van energie kunnen gaan. Het meet hoe bruikbare energie afneemt, een proces dat ook wel wordt aangeduid als 'wanorde',
Daarom zijn sommige chemische transformaties mogelijk terwijl anderen nooit zullen gebeuren. Je kunt bijvoorbeeld met zekerheid vaststellen dat als je een ijsklontje in een kop koffie doet het ijsklontje zal smelten, terwijl de koffie nooit zal bevriezen.
De principes van de thermodynamica zijn de principiële wetten achter temperatuur, energie en entropie
Ben je op zoek naar een uitgebreide persoonlijke wiskunde b uitleg? Vraag om hulp van een van onze gespecialiseerde privéleraren bij jou in de buurt!
10. De Schrödinger-vergelijking
De Schrödinger-vergelijking, uitgevonden door de Oostenrijkse natuurkundige Erwin Schrödinger in 1925, is een fundamentele vergelijking in de kwantummechanica.
Zoals Einstein's relativiteitstheorie hielp het universum op een grote schaal te verklaren, zo werpt deze vergelijking licht op het gedrag van atomen en subatomische deeltjes. De Schrödinger-vergelijking legt uit hoe deeltjes door de tijd heen veranderen. Het beschrijft de verschillende staten van een deeltje, waardoor het mogelijk is om elk deeltje in elke staat te beschrijven.
Deze vergelijking is eigenlijk een filosofisch vraagstuk: bestaat materie door de aanwezigheid van verschillende fysieke staten (vloeistof, gas, vaste materie)? De toepassing van deze vergelijking kan gevonden worden in de moderne kernenergie, in computers en bij lasers.
Als deze wiskundigen je verbaasd hebben, kijk dan ook eens naar onze blog over hoe wiskunde terugkomt in kunst om te zien hoe hun theorieën op praktische en creatieve manieren zijn toegepast.

Zoals we kunnen zien, hebben wiskundige vergelijkingen door de geschiedenis heen en vooral sinds de 18e eeuw ons begrip van de wereld waarin we leven getransformeerd, en daarmee onze mogelijkheid om wiskundige problemen op te lossen. Zelfs in sport wordt wiskunde toegepast!
Dat helpt ons elke dag in ons dagelijks leven, tijdens wiskundelessen of bij meer directe toepassingen.
Wat zal onze nieuwe grote wiskundige uitvinding worden? Welke nieuwe wiskundige ontdekking zal de huidige concepten van het leven compleet overhoop gooien?
Zelf verder gaan met wiskunde
Wil je meer van deze formules leren? Of ben je benieuwd naar andere interessante wiskundige formules? Dan kun je met een aantal uur aan privé les al heel wat verder raken. Via het online platform van Superprof vind je op een snelle en eenvoudige manier een leraar die bij je past. Wacht dus niet langer en ga op wiskundige ontdekkingsreis!
Welke wiskundige formule vind jij het meest fascinerend?
Samenvatten met AI















De elektrische flux door een gesloten oppervlak is enkel nul indien dat oppervlak geen netto lading omsluit. De magnetische flux door een gesloten oppervlak is wel altijd nul omdat er geen magnetische ladingen bestaan.